Overfull graph
In graph theory, an overfull graph is a graph whose size is greater than the product of its maximum degree and its order floored, i.e. 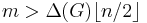 where m is the size of G,
where m is the size of G, 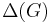 is the maximum degree of G, and n is the order of G. The concept of an overfull subgraph, an overfull graph that is a subgraph, immediately follows. An alternate, stricter definition of an overfull subgraph S of a graph G requires
is the maximum degree of G, and n is the order of G. The concept of an overfull subgraph, an overfull graph that is a subgraph, immediately follows. An alternate, stricter definition of an overfull subgraph S of a graph G requires  .
.
Contents |
Properties
A few properties of overfull graphs:
- Overfull graphs are of odd order.
- Overfull graphs are class 2. That is, they require at least Δ + 1 colors in any edge coloring.
- A graph G, with an overfull subgraph S such that
 , is of class 2.
, is of class 2.
Overfull conjecture
In 1986, Chetwynd and Hilton posited the following conjecture that is now known as the overfull conjecture.[1]
- A graph G with
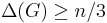 is class 2 if and only if it has an overfull subgraph S such that
is class 2 if and only if it has an overfull subgraph S such that  .
.
This conjecture, if true, would have numerous implications in graph theory, including the 1-factorization conjecture.[2]
Algorithms
For graphs in which 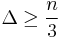 , there are at most three induced overfull subgraphs, and it is possible to find an overfull subgraph in polynomial time. When
, there are at most three induced overfull subgraphs, and it is possible to find an overfull subgraph in polynomial time. When 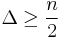 , there is at most one induced overfull subgraph, and it is possible to find it in linear time.[3]
, there is at most one induced overfull subgraph, and it is possible to find it in linear time.[3]
References
- ^ Chetwynd, A. G.; Hilton, A. J. W. (1986), "Star multigraphs with three vertices of maximum degree", Mathematical Proceedings of the Cambridge Philosophical Society 100 (2): 303–317, doi:10.1017/S030500410006610X, MR848854.
- ^ Chetwynd, A. G.; Hilton, A. J. W. (1989), "1-factorizing regular graphs of high degree—an improved bound", Discrete Mathematics 75 (1-3): 103–112, doi:10.1016/0012-365X(89)90082-4, MR1001390.
- ^ Niessen, Thomas (2001), "How to find overfull subgraphs in graphs with large maximum degree. II", Electronic Journal of Combinatorics 8 (1): Research Paper 7, MR1814514, http://www.combinatorics.org/Volume_8/Abstracts/v8i1r7.html.